Как-то раз, обсуждая с одногруппницей тему ее диплома, я посоветовал ей отличную статью Data alignment: Straighten up and fly right, посвященную выравниванию данных в оперативной памяти. Т. к. с английским у нее дела обстоят не очень хорошо, она попросила меня перевести статью на русский язык. Переведя статью, я решил, что незачем добру пропадать, и поэтому с разрешения автора выкладываю сюда перевод. Перевод довольно вольный, но в то же время достаточно точный. Вообщем, буду рад, если кому-нибудь пригодится.
Выравнивание данных - очень важное понятие, которое должен принимать во внимание каждый программист, работающий с памятью напрямую. Выравнивание данных влияет на скорость выполнения ваших программ и на то, будут ли они вообще работать. Понимание основных принципов, заложенных в данном понятии, объясняет на первый взгляд странное поведение некоторых процессоров.
Гранулярность доступа к памяти
Программисты привыкли думать о памяти, как о простом массиве байтов. В языке C и его языках-наследникахchar* всегда означало "блок данных", и даже в Java™ есть тип byte[] для представления "сырых" данных в памяти.Рис. 1. Как программисты видят память

Однако, процессор в вашем компьютере считывает данные из памяти блоками размером отнюдь не в одни байт. Считывание данных производится блоками по 2, 4, 8, 16 или даже 32 байта. Далее размер таких блоков мы будем называть гранулярностью доступа к памяти.
Рис. 2. Как эту же память видят процессоры

Разница в том, как программисты видят память, и как процессоры на самом деле с ней работают, приводит к интересным последствиям, которым и посвящена данная статья.
Если вы не понимаете, какое влияние выравнивание данных способно оказать на ваше программное обеспечение, то возможно возникновение следующих проблем в работе вашего ПО (в порядке возрастания пагубного воздействия):
- Приложение будет работать медленнее.
- Приложение может "зависнуть".
- Операционная система может внезапно аварийно завершиться.
- Приложение будет работать непредсказуемо, что в итоге может привести к порче ваших данных.
Что такое выравнивание
Чтобы проиллюстрировать принципы, лежащие в основе выравнивания данных, выполним небольшую программу и посмотрим, какое влияние на нее будет оказывать гранулярность доступа к памяти. Программа предельно проста: сначала считываем в регистр 4 байта с адреса 0, а затем считываем в тот же регистр 4 байта с адреса 1.Для начала посмотрим, как наша программа будет работать на процессоре с однобайтовой гранулярностью доступа к памяти:
Рис. 3. 1-байтовая гранулярность доступа к памяти
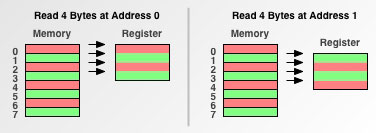
Здесь мы видим то, что и ожидает увидеть любой программист, руководствующийся базовыми представлениями о том, как работает оперативная память: при считывании 4 байт с адреса 1 процессор делает те же 4 операции доступа к памяти, что и при считывании данных с адреса 0. А теперь давайте посмотрим, как наша программа будет работать на процессоре с гранулярностью доступа к памяти в 2 байта (примером такого процессора является классический 68000):
Рис. 4. 2-байтовая гранулярность доступа к памяти

При чтении данных с адреса 0 процессору с 2-байтовой гранулярностью требуется в два раза меньше операций доступа к памяти, чем процессору с 1-байтовой гранулярностью. Считывание двух байтов за одну операцию доступа к памяти производится быстрее, чем считывание тех же двух байтов за две операции доступа к памяти (см. Разработка на PC и производительность — Memory Latency - прим. переводчика), так что производители процессоров могут добиться заметного увеличения производительности путем уменьшения операций доступа к памяти, увеличив при этом гранулярность.
Однако заметьте, что происходит, когда мы считываем данные с адреса 1. Т. к. адрес не кратен размеру считываемых данных, процессору приходится выполнять лишнюю работу, считывая при этом 6 байт вместо 4. Такой адрес называется невыровненным. При доступе к данным по невыровненным адресам процессору приходится делать лишние обращения к памяти, что в итоге приводит к снижению скорости работы программы.
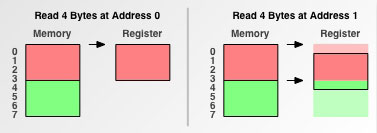
Теперь же давайте посмотрим, что произойдет, если запустить нашу программу на процессоре с гранулярностью доступа к данным в 4 байта (таком как 68030 или PowerPC® 601):
Рис. 5. 4-байтовая гранулярность доступа к памяти
 style="cursor: pointer; width: 377px; height: 133px;">
style="cursor: pointer; width: 377px; height: 133px;">Процессор с гранулярностью доступа к памяти в 4 байта может считать требуемый нам объем информации с выровненного адреса за одну операцию доступа к памяти. Однако считывание данных с невыровненного адреса в два раза увеличивает количество операций доступа к памяти, требуемых для считывания того же объема данных.
Теперь, когда мы показали что такое выравнивание, перейдем к рассмотрению того, как оно влияет на работу вашей программы.
"Ленивые" процессоры
Процессор вынужден прибегать к некоторым дополнительным действиям при обработке инструкции на доступ к данным с невыровненного адреса. Вернемся к нашему примеру со считыванием 4 байт с адреса 1 на процессоре с гранулярностью в 4 байта:Рис. 6. Обработка процессором команды на доступ к данным по невыровненному адресу
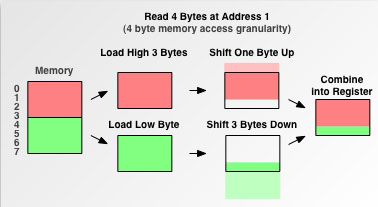
Процессор вынужден считать блок данных, на который приходится невыровненный адрес, сдвинуть полученные данные, считать следующий за ним блок данных, в котором содержится оставшийся один байт интересующих нас данных, сдвинуть полученные данные, объединить вместе с данными первого блока и поместить их в регистр, т. е. проделать довольно большой объем работы.
Некоторые процессоры просто не выполняют эту работу.
Классический 68000 был процессором с гранулярностью в 2 байта и не имел соответствующей логики обработки невыровненных данных. Если он сталкивался с командой на обращение к данным по невыровненному адресу, то просто генерировал исключение, а, к примеру, классическая Mac OS не обрабатывала данное исключение должным образом и выдавала пользователю сообщение с требованием перезагрузить систему.
Более поздние процессоры серии 680x0, к примеру 68020, утратили данное ограничение и выполняли всю необходимую работу. Это объясняет, почему некоторые старые программы, отлично работающие на 68020, аварийно завершались на 68000, и также объясняет тот факт, почему раньше программисты, писавшие программы для Mac OS, инициализировали указатели странными адресами - если на классической Mac OS управление доходило до разыменования указателя, которому не был присвоен адрес реально существующих данных, система немедленно передавала управление отладчику. Впоследствии они могли просмотреть стек вызова функций и определить, где произошла ошибка.
Каждый процессор имеет ограниченное количество транзисторов, которое может быть в нем использовано. Добавление поддержки доступа к невыровненным данным вынуждает инженеров уменьшать количество транзисторов, предназначенных для обеспечения работы остальных подсистем процессора, что может сделать невозможным добавление каких-либо дополнительных возможностей в процессор или несколько снизить скорость его работы.
Примером процессора, который ради скорости жертвует поддержкой доступа к невыровненым данным, является MIPS. MIPS - отличный пример процессора, в котором не реализованы многие специфические возможности во имя обеспечения более высокого быстродействия.
PowerPC использует следующий подход: все современные PowerPC-процессоры имеют поддержку доступа к невыровненным 32-битовым целочисленным значениям, и хотя пользователям и приходится платить за доступ к невыровненным данным некоторым снижением производительности, оно довольно невелико.
С другой стороны, современные PowerPC-процессоры не включают в себя поддержку доступа к 64-битовым вещественным числам, и если процессор встречает команду на доступ к такому числу с невыровненного адреса, то он генерирует исключение, передавая тем самым управление операционной системе и давая ей возможность на софтверном уровне выполнить всю необходимую работу. Это решает проблему, но, естественно, выполняется значительно медленнее, чем если бы все необходимые операции выполнял процессор.
Скорость
Напишем несколько тестов, которые проиллюстрируют нам падение производительности при обращении к невыровненным данным. Тесты предельно простые: считываем число, изменяем его знак и записываем полученное значение обратно. Числа считываются из и записываются в 10 Мб буфер. При тестировании изменяются следующие значения:- Размер чисел, которыми обрабатывается буфер. Сначала буфер обрабатывается 1-байтовыми числами, затем 2-, 4- и 8-байтовыми.
- Выравнивание буфера. Мы изменяем выравнивание буфера, увеличивая указатель на него, и запускаем тест снова.
Тесты выполнялись на 800 MHz PowerBook G4. Чтобы уменьшить влияние операционной системы и других программ на их результаты, каждый тест был запущен 10 раз, и было взято среднее значение от полученных результатов. Первый тест - работа с 1-байтовыми числами:
Листинг 1. Обработка 1-байтовыми числами
void Munge8( void *data, uint32_t size ) {
uint8_t *data8 = (uint8_t*) data;
uint8_t *data8End = data8 + size;
while( data8 != data8End )
*data8++ = -*data8;
}Для выполнения данной функции в среднем потребовалось 67 364 микросекунды. Теперь изменим ее для работы с 2-байтовыми числами (в таком случае ей потребуется выполнить в два раза меньше операций доступа к данным):
Листинг 2. Обработка 2-байтовыми числами
void Munge16( void *data, uint32_t size ) {
uint16_t *data16 = (uint16_t*) data;
uint16_t *data16End = data16 + (size >> 1); /* Divide size by 2. */
uint8_t *data8 = (uint8_t*) data16End;
uint8_t *data8End = data8 + (size & 0x00000001); /* Strip upper 31 bits. */
while( data16 != data16End )
*data16++ = -*data16;
while( data8 != data8End )
*data8++ = -*data8;
}Этой функции в среднем потребовалось 48 765 микросекунд для обработки того же 10 Мб буфера, что на 38% быстрее чем в предыдущем примере. Однако, этот буфер был выровнен. Если же мы возьмем невыровненный буфер, то время работы функции увеличится до 66 385 микросекунд, т. е. 27% времени будет уходить на обеспечение работы с невыровненными данными. Следующий график демонстрирует, как меняется производительность при обработке выровненного и невыровненного буфера:
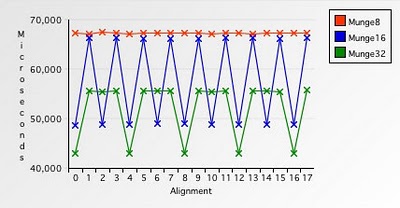
Рис. 7. Сравнение времени обработки 1-байтовыми числами с временем обработки 2-байтовыми числами
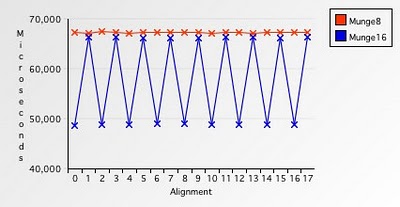
Как видно из графика, обработка 1-байтовыми числами заняла довольно много времени. В то же время на обработку 2-байтовыми числами требуется значительно меньше времени, но только до тех пор, пока буфер выровнен по 2-байтовой границе, в противном случае 27% времени мы будем тратить впустую.
А теперь посмотрим, что будет, если мы попробуем обрабатывать данные четырехбайтовыми числами:
Листинг 3. Обработка 4-байтовыми числами
void Munge32( void *data, uint32_t size ) {
uint32_t *data32 = (uint32_t*) data;
uint32_t *data32End = data32 + (size >> 2); /* Divide size by 4. */
uint8_t *data8 = (uint8_t*) data32End;
uint8_t *data8End = data8 + (size & 0x00000003); /* Strip upper 30 bits. */
while( data32 != data32End )
*data32++ = -*data32;
while( data8 != data8End )
*data8++ = -*data8;
}Обработка выровненного буфера заняла 43 043 микросекунды. Невыровненный буфер обрабатывался 55 775 микросекунд. Таким образом, получается, что на данной тестовой машине невыровненные 4-байтовые числа обрабатываются медленнее выровненных 2-байтовых чисел:
Рис. 8. Сравнение времени обработки 1-байтовыми, 2-байтовыми и 4-байтовыми числами
А теперь плохая новость: попробуем обработать тот же буфер 8-байтовыми числами:
Листинг 4. Обработка 8-байтовыми числами
void Munge64( void *data, uint32_t size ) {
double *data64 = (double*) data;
double *data64End = data64 + (size >> 3); /* Divide size by 8. */
uint8_t *data8 = (uint8_t*) data64End;
uint8_t *data8End = data8 + (size & 0x00000007); /* Strip upper 29 bits. */
while( data64 != data64End )
*data64++ = -*data64;
while( data8 != data8End )
*data8++ = -*data8;
}Munge64()
обработала выровненный буфер за 39 085 микросекунд - это на 10% быстрее
чем при обработке 4-байтовыми числами. Однако обработка 8-байтовыми
числами невыровненного буфера заняла целых 1 841 155 микросекунд - на
два порядка медленнее обработки выровненных данных!Что произошло? Т. к. в современных PowerPC нет аппаратной поддержки доступа к невыровненным восьмибайтовым числам, процессор генерирует исключение при каждом обращении к такому числу. Операционная система перехватывает исключение и выполняет выравнивание вручную. Следующий график иллюстрирует падение производительности, и когда оно происходит:
Рис. 9. Сравнение времени работы при обработке числами различного размера
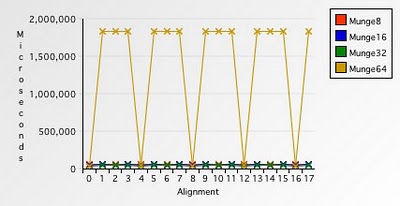
Падение быстродействия при обращении к невыровненным 2- и 4-байтовым числам просто меркнет на фоне падения быстродействия при обращении к невыровненным 8-байтовым числам, поэтому "отрежем" его верхнюю часть:
Рис. 10. Сравнение времени работы при обработке числами различного размера #2
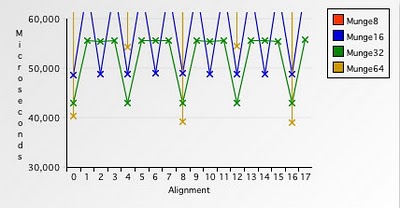
А теперь более пристально посмотрим на график и сравним скорость выполнения программы при обращении к 8-байтовым числам, выровненным по 4-байтовой границе:
Рис. 11. Сравнение времени работы при обработке числами различного размера #3
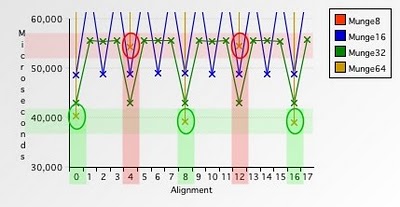
Заметьте, что обращение к 8-байтовым числам, выровненным по 4-байтовой и 12-байтовой границе, медленнее, чем чтение тех же данных, 4- или даже 2-байтовыми числами. Несмотря на то, что PowerPC имеет аппаратную поддержку работы с 8-байтовыми числами, выровненными по 4-байтовой границе, вам все равно приходится платить временем выполнения программы за доступ по адресам, не кратным восьми. К счастью, эта плата не настолько велика, как при доступе к 8-байтовым числам, выровненным по 1-, 2-, 3-, 5-, 6- и 7-байтовым границам, но мораль в том, что доступ к невыровненной памяти быстрее при работе с числами меньшего размера.
Атомарность
Все современные процессоры предоставляют инструкции атомарного доступа к данным. Эти специальные инструкции являются ключевыми при реализации различных примитивов синхронизации, необходимых для контроля доступа к данным из нескольких одновременно выполняющихся программ (потоков). Как нетрудно догадаться по их имени, выполнение атомарных инструкций не должно прерываться во время их выполнения - именно это свойство делает их просто незаменимыми при реализации объектов синхронизации.Отсюда вытекает требование передавать атомарным инструкциям только адреса, выровненные как минимум по 4-байтовой границе - иначе корректность их работы не может быть гарантирована. Причина этого кроется в тесной зависимости атомарных инструкций от подсистемы виртуальной памяти.
Если адрес не выровнен, то требуется как минимум две операции доступа к памяти. Но что произойдет, если требуемые нам данные находятся на границе двух страниц виртуальной памяти? Вполне вероятна ситуация, когда первая страница будет находиться в оперативной памяти, а вторая будет выгружена на диск. В таком случае при доступе к данным во время выполнения атомарной инструкции будет сгенерировано прерывание Page fault, что приведет к передаче управления подсистеме виртуальной памяти, отвечающей за подкачку выгруженных на диск страниц в память, а, следовательно, нарушению атомарности инструкции. Чтобы устранить возможность возникновения подобной ситуации, и 68K, и PowerPC требуют, чтобы все данные, к которым впоследствии будет производиться атомарный доступ, были выровнены по 4-байтовой границе.
К сожалению, PowerPC не генерирует исключение, когда встречает инструкцию атомарной записи по невыровненному адресу. Вместо этого, он просто оставляет данные без изменения. Это может привести к довольно неприятным последствиям, т. к. многие атомарные функции написаны так, что после неудачной записи повторяют свою попытку снова и снова в предположении, что в данном случае ресурсом завладел кто-то другой, что в итоге приводит к "зависанию" программы.
Выравнивание в структурах
Рассмотрим следующую структуру:Листинг 5. Обычная структура
typedef struct {
char a;
long b;
char c;
} Struct;Как вы думаете, какой размер данная структура занимает в памяти компьютера? Многие программисты ответят "6 байт". Это вполне логично: один байт для
a, четыре байта для b и еще один байт для c. 1 + 4 + 1 = 6. Если следовать данным рассуждениям, то такая структура должна располагаться в памяти следующим образом:| Тип поля | Имя поля | Смещение поля | Размер поля | Конец поля |
char | a | 0 | 1 | 1 |
long | b | 1 | 4 | 5 |
char | c | 5 | 1 | 6 |
| Всего байт: | 6 | |||
Однако, если вы "попросите" ваш компилятор выдать размер данной структуры при помощи
sizeof( Struct ),
то, скорее всего, получите величину больше чем 6, вероятнее всего 8, а
возможно даже и целых 24 байта. Этому есть две причины: обратная
совместимость и эффективность.Итак, обратная совместимость. Помните 68000-процессор с гранулярностью доступа к памяти в два байта, который генерировал исключение при обращении к невыровненным адресам? Если бы при такой организации структуры вы попытались обратиться к полю
b, то вы обратились бы по невыровненному адресу. В итоге,
если отладчик у вас не установлен, Mac OS отобразила бы вам диалог с
сообщением о критической ошибке и всего одной кнопкой
"Перезагрузиться". Вряд ли такое сообщение доставит много радости
пользователю, особенно если у него остались несохраненные данные!Поэтому, вместо того, чтобы располагать поля в структурах так, как программист видит их в описании структуры, компилятор вставляет "лишние" данные между ее полями, чтобы все поля располагались по выравненным адресам:
| Тип поля | Имя поля | Смещение поля | Размер поля | Конец поля |
char | a | 0 | 1 | 1 |
| выравнивание | 1 | 1 | 2 | |
long | b | 2 | 4 | 6 |
char | c | 6 | 1 | 7 |
| выравнивание | 7 | 1 | 8 | |
| Всего байт: | 8 | |||
Сегодня, когда 68020 производится с поддержкой доступа к невыровненным данным, это может показаться излишним, но не надо забывать про производительность.
А вторая причина - как раз производительность. Сегодня PowerPC хорошо работает с данными, выравненными по 2-байтовой границе, но еще лучше он работает с данными, выравненными по 4-байтовой границе. Вам, возможно, и нет необходимости заботиться о классическом 68000, но о потенциальном снижении производительности на два порядка при доступе к невыровненным полям типа
double явно стоит! Именно поэтому компиляторы в обязательном порядке самостоятельно выравнивают все поля внутри структур.Заключение
Итак, если вы не знаете, что такое выравнивание, и какое влияние оно оказывает на работу ваших программ то:- Ваши программы могут работать значительно медленнее, чем могли бы, если они делают много обращений к невыровненным данным, т. к. при их выполнении процессор будет вынужден выполнять лишнюю работу.
- Ваши программы могут "зависать", если вы размещаете объекты синхронизации по невыровненным адресам.
- Есть вероятность, что вы не оптимально размещаете поля внутри структур, что приводит к некоторому снижению скорости работы программы, а также может быть критично в случае большого дефицита оперативной памяти (прим. переводчика).